Distribution of Words
In order to design the index files for a text search engine,
it is helpful to have some information about the relationship
between the number of words in some body of text and the amount
of data. The graphs below present some data on this topic. The
source data was a sample of articles from the Reuters News Service.
The sample had just over 75 Megabytes comprising around 10.5
million words. The "words" were computed as whitespace-delimited
strings of characters. Leading and trailing punctuation was
removed (so that each word begins and ends with either a letter
or a digit). "Words" that did not contain a letter were discarded.
Thus, '4x4' and 'command.com' count as words, but '$100' does not.
Upper case letters (A-Z) were changed to lower case (a-z), so that
the words 'The' and 'the' were not counted as distinct words.
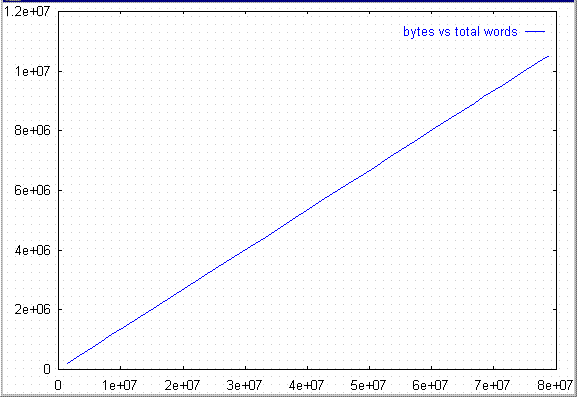
This is a graph of the number of bytes vs total number of words
that appeared in the Reuters data. Notice that the increase is
very close to linear. This is not surprising. In a well-edited
corpus like Reuters data, the average number of characters per
word can be expected to hold fairly constant.
This is a graph of total words in the corpus vs the number of unique
words. The same Reuters data was used here. Among the 10.5 million
words, only about 79,000 words were distinct.
For reference, there is also a plot of the function y = 25 * sqrt(x). Notice how similar the two curves are. There is nothing special about the number 25. It was chosen to provide a close fit for this data. For other data sets, other numbers may provide a better fit.


